攻防世界-crypto

一、base64

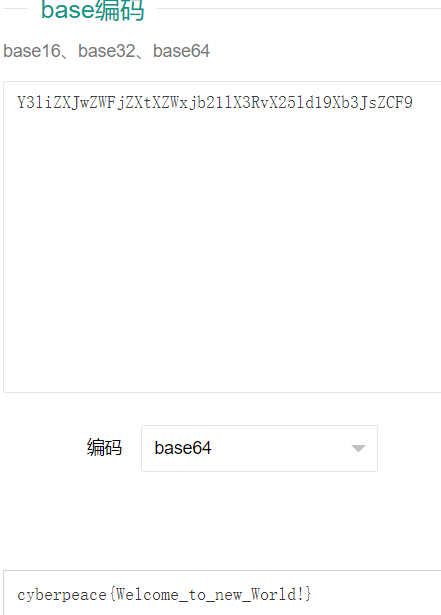
题目：Y3liZXJwZWFjZXtXZWxjb21lX3RvX25ld19Xb3JsZCF9

1、知识补充

一、什么是Base64?
百度百科中对Base64有一个很好的解释：“Base64是网络上最常见的用于传输8Bit字节码的编码方式之一，Base64就是一种基于64个可打印字符来表示二进制数据的方法”。

什么是“可打印字符”呢？为什么要用它来传输8Bit字节码呢？在回答这两个问题之前我们有必要来思考一下什么情况下需要使用到Base64？Base64一般用于在HTTP协议下传输二进制数据，由于HTTP协议是文本协议，所以在HTTP协议下传输二进制数据需要将二进制数据转换为字符数据。然而直接转换是不行的。因为网络传输只能传输可打印字符。什么是可打印字符？在ASCII码中规定，0-31、127这33个字符属于控制字符，32-126这95个字符属于可打印字符，也就是说网络传输只能传输这95个字符，不在这个范围内的字符无法传输。那么该怎么才能传输其他字符呢？其中一种方式就是使用Base64。

Base64，就是使用64个可打印字符来表示二进制数据的方法。Base64的索引与对应字符的关系如下表所示：

​ img

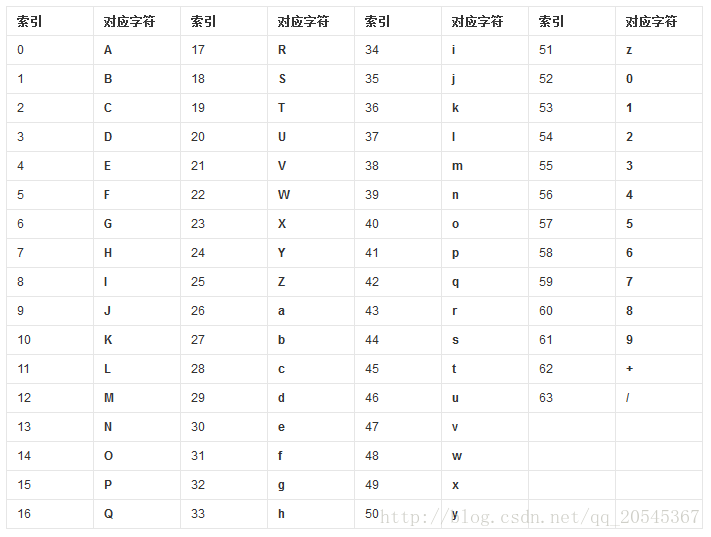
也就是说，如果将索引转换为对应的二进制数据的话需要至多6个Bit。然而ASCII码需要8个Bit来表示，那么怎么使用6个Bit来表示8个Bit的数据呢？6个Bit当然不能存储8个Bit的数据，但是46个Bit可以存储38个Bit的数据啊！如下表所示：

​ img

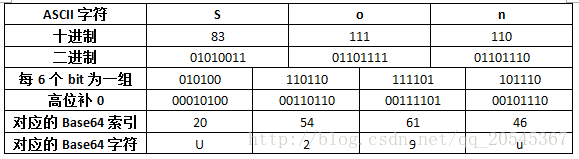
可以看到“Son”通过Base64编码转换成了“U29u”。这是刚刚好的情况，3个ASCII字符刚好转换成对应的4个Base64字符。但是，当需要转换的字符数不是3的倍数的情况下该怎么办呢？Base64规定，当需要转换的字符不是3的倍数时，一律采用补0的方式凑足3的倍数，具体如下表所示：

img

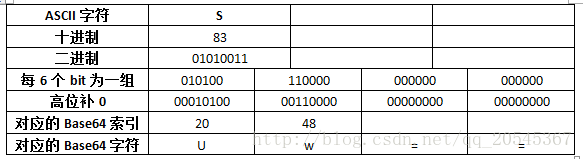
每6个Bit为一组，第一组转换后为字符“U”，第二组末尾补4个0转换后为字符“w”。剩下的使用“=”替代。即字符“S”通过Base64编码后为“Uw==”。这就是Base64的编码过程。

2、解答

使用在线解答工具：CTF在线工具-在线base编码|在线base解码|base16编码|base32编码|base64编码 (hiencode.com)

3、注意

如何判断是否为base64加密?

可以通过判断字符串是否具有base64编码的特点来确定。那么base64编码之后的字符串具有哪些特点：

  • 字符串只可能包含A-Z，a-z，0-9，+，/，=字符
  • 字符串长度是4的倍数
  • =只会出现在字符串最后，可能没有或者一个等号或者两个等号

参考：https://blog.csdn.net/jinweilin/article/details/79587314

二、Caesar（凯撒密码）

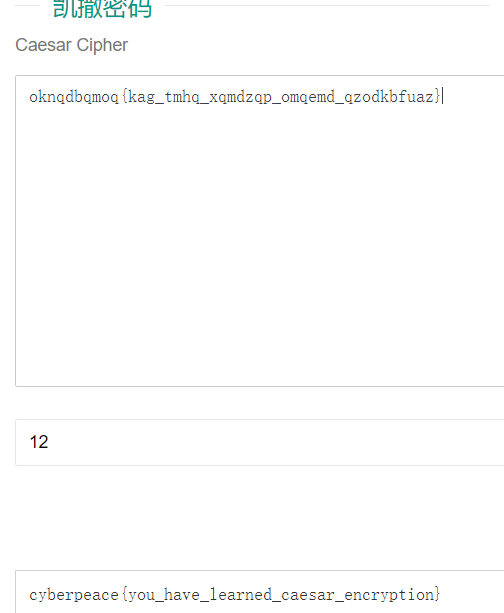
题目：oknqdbqmoq{kag_tmhq_xqmdzqp_omqemd_qzodkbfuaz}

1、知识补充

一、 什么是凯撒密码？

二、 凯撒密码的加密过程

用凯撒密码加密，密钥是3

三 、凯撒密码的解密过程

用凯撒密码解密，密钥也是3

四 、暴力破解凯撒密码

在凯撒密码中，密钥就是字母表平移的数字。由于字母表只有26个字母，因此加密用的密钥只有0到25共26种（平移0个字母实际相对于没有加密）。

按顺序将这26种密钥都尝试一遍。

2、解答

使用在线解答工具CTF在线工具-在线凯撒密码加密|在线凯撒密码解密|凯撒密码算法|Caesar Cipher (hiencode.com)

通过观察题干，由凯撒密码是通过移位实现的，正常应该是c开头，而题目是o开头，c~o是12位，所以key=12

3、注意

特定恺撒密码名称

根据偏移量的不同，还存在若干特定的恺撒密码名称：

  • 偏移量为10：Avocat(A→K)
  • 偏移量为13：ROT13
  • 偏移量为-5：Cassis (K 6)
  • 偏移量为-6：Cassette (K 7)

如何看出凯撒密码

（1）攻击者知道（或者猜测）密码中使用了某个简单的替换加密方式，但是不确定是恺撒密码；

（2）攻击者知道（或者猜测）使用了恺撒密码，但是不知道其偏移量。

对于第一种情况，攻击者可以通过使用诸如频率分析或者样式单词分析的方法， 马上就能从分析结果中看出规律，得出加密者使用的是恺撒密码。

对于第二种情况，解决方法更加简单。 由于使用恺撒密码进行加密的语言一般都是 字母文字 系统，因此密码中可能是使用的偏移量也是有限的，例如使用26个字母的 英语 ，它的偏移量最多就是25（偏移量26等同于偏移量0，即明文；偏移量超过26，等同于偏移量1-25）。 因此可以通过 穷举法 ，很轻易地进行破解。

三、Morse

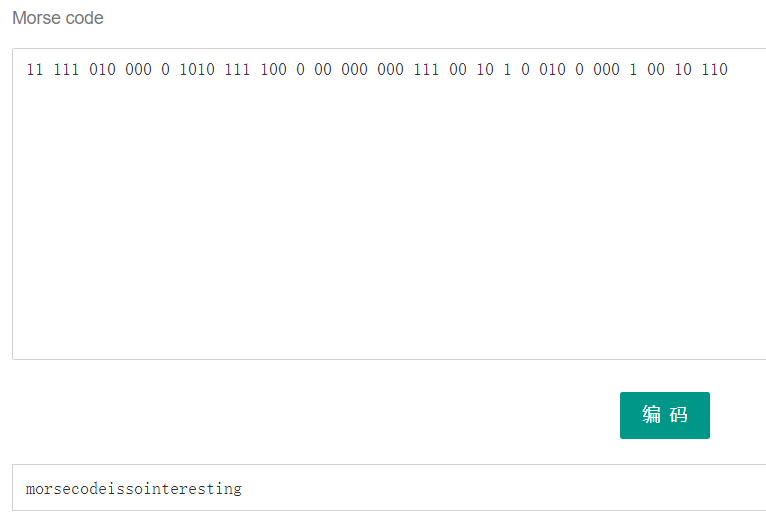
题目：11 111 010 000 0 1010 111 100 0 00 000 000 111 00 10 1 0 010 0 000 1 00 10 110

1、知识补充

摩尔斯电码（又译为摩斯密码，Morse code）是一种时通时断的信号代码，通过不同的排列顺序来表达不同的英文字母、数字和标点符号。它发明于1837年，发明者有争议，是美国人塞缪尔·莫尔斯或者艾尔菲德·维尔。 摩尔斯电码是一种早期的数字化通信形式，但是它不同于现代只使用零和一两种状态的二进制代码，它的代码包括五种： 点、划、点和划之间的停顿、每个字符之间短的停顿、每个词之间中等的停顿以及句子之间长的停顿。
现在已经很少用了（但在解码方面还是有很大影响力）

传递时的规则：
摩尔斯电码由两种基本信号组成：短促的点信号“·”，读“滴”；保持一定时间的长信号“—”，读“嗒”。间隔时间：滴=1t，嗒=3t，滴嗒间=1t，字符间=3t，单词间=7t。

实现：
其实很简单，只是需要一一对应即可，以下便是常用的摩斯密码对应表。
至于为什么是这样对应的，你们可以去看一下一篇英文文章中出现每个字母的频率（或次数），为了节约传输字节，所以根据出现次数越多的编码越短（即E、T出现次数最多），所以形成了这样的规定，当然自己也可以更改成自己的规则（创建自己的字典），别人就破译不出来了。

代码：
解码时需要知道字符串和分割标识符

2、解答

摩斯密码使用 .、- 来表示不同含义，这里只用 0和1

结果：用·表示0，-表示0

image-20220311102234471

3、注意

反复出现两个、三个字符，考虑摩斯密码

四、幂数加密

题目：8842101220480224404014224202480122

flag为cyberpeace{你解答出的八位大写字母}

1、知识补充

二进制幂数加密法，由于英文字母只有26个字母。只要2的0、1、2、3、4、5次幂就可以表示31个单元。通过用二进制幂数表示字母序号数来加密。

二进制幂数加密法就是应用这个原理，由于英文字母只有26个字母，由公式可知，只要2的0、1、2、3、4、5次幂就可以表示31个单元。通过用二进制幂数表示字母序号数来加密。例如

明文： d o n o t p u l l a l l y o u r e g g s i n o n e b a s k e t

字母序号：4 15 14 15 20 16 21 12 12 1 12 12 25 15 21 18 5 7 7 19 9 14 15 14 5 2 1 19 11 5 20

由于4=2^2 所以D加密过之后是2；15=2^0+2^1+2^2+2^3所以O加密后是0123。同理得到上述明文的加密后的密文

密文：2 0123/123 0123 24/4 024 23 23/0 23 23/034 0123 024 14/02 012 012 014/03 123 /0123 123 02/1 0 014 013 02 24

2、解答

##云影密码 此密码运用了1248代码，

原理很简单，有了1，2，4，8这四个简单的数字，你可以以加法表示出0-9任何一个数字，例如0=28，7=124，9=18。 这样，再用1-26来表示A-Z，就可以用作密码了。 为了不至于混乱，我个人引入了第五个数字0，来用作间隔，以避免翻译错误，所以还可以称“01248密码”。

题目上说结果为八位大写字母，所以要把txt文件中的数字分为8组，按0位间隔正好八组

8842101220480224404014224202480122

88421 0122 048 02244 04 0142242 0248 0122

23 5 12 12 4 15 14 5
W E L L D O N E

代码实现：

1
2
3
4
5
6
7
8
9
10
a = "8842101220480224404014224202480122"
a = a.split("0")
flag = ''
for i in range(0, len(a)):
    str = a[i]
    sum = 0
    for i in str:
        sum += int(i)
    flag += chr(sum + 64)
print (flag)

3、注意

只有‘01248’出现时要注意幂数加密

五、Railfence

题目：ccehgyaefnpeoobe{lcirg}epriec_ora_g

是一副农家小院的 图画，上面画着一个农妇在栅栏里面喂5只小鸡

1、知识补充

栅栏密码的两种加密方式：

第一种常规的顺序加密：

明文：123456789

加密栏数：3

加密过程：
1.把明文的元素从上到下排成3行
1 4 7
2 5 8
3 6 9
2.再把3排结果从上到下拼接起来，即加密结果为
147258369

第二种回形针式加密（W型）：

明文：123456789

加密栏数：3

加密过程：
1.把明文的元素先从上到下排列，再从下到上排列，依次类推，直到把明文全部排列完为止

1 5 9
2 4 6 8
3 7

2.再把3排结果从上到下拼接起来，即加密结果为
159246837

PS:因为排列的形态像一个字母”W”，所以被称为W型加密。

2、解答

由{}里有5个字母，根据栅栏加密的规则，猜测key=5

image-20220313152457995

3、注意

观察题目发现题目包含{}括号，flag应有元素齐全，所以仅是内容本身进行变化，且题干为栅栏的意思

六、不仅仅是Morse

题目：—/.-/-.—/..—.-/-…/./..—.-/…./.-/…-/./..—.-/.-/-./—-/-/…././.-./..—.-/-.././-.-./—-/-.././…./…./…./…./.-/.-/.-/.-/.-/-…/.-/.-/-…/-…/-…/.-/.-/-…/-…/.-/.-/.-/.-/.-/.-/.-/.-/-…/.-/.-/-…/.-/-…/.-/.-/.-/.-/.-/.-/.-/-…/-…/.-/-…/.-/.-/.-/-…/-…/.-/.-/.-/-…/-…/.-/.-/-…/.-/.-/.-/.-/-…/.-/-…/.-/.-/-…/.-/.-/.-/-…/-…/.-/-…/.-/.-/.-/-…/.-/.-/.-/-…/.-/.-/-…/.-/-…/-…/.-/.-/-…/-…/-…/.-/-…/.-/.-/.-/-…/.-/-…/.-/-…/-…/.-/.-/.-/-…/-…/.-/-…/.-/.-/.-/-…/.-/.-/-…/.-/.-/-…/.-/.-/.-/.-/-…/-…/.-/-…/-…/.-/.-/-…/-…/.-/.-/-…/.-/.-/-…/.-/.-/.-/-…/.-/.-/-…/.-/.-/-…/.-/.-/-…/.-/-…/.-/.-/-…/-…/.-/-…/.-/.-/.-/.-/-…/-…/.-/-…/.-/.-/-…/-…/.-

1、知识补充

摩斯电码会加上分隔符，具体相关知识见Morse

培根密码，培根所用的密码是一种本质上用二进制数设计的，没有用通常的0和1来表示，而是采用a和b

一、培根密码加密方式

1
2
3
4
5
6
7
8
9
10
11
12
第一种方式：
A aaaaa B aaaab C aaaba D aaabb E aabaa F aabab G aabba H aabbb I abaaa J abaab
K ababa L ababb M abbaa N abbab O abbba P abbbb Q baaaa R baaab S baaba T baabb
U babaa V babab W babba X babbb Y bbaaa Z bbaab

第二种方式
a AAAAA   g AABBA    n ABBAA   t BAABA
b AAAAB   h AABBB    o ABBAB   u-v BAABB
c AAABA   i-j ABAAA  p ABBBA   w BABAA
d AAABB   k ABAAB    q ABBBB   x BABAB
e AABAA   l ABABA    r BAAAA   y BABBA
f AABAB   m ABABB    s BAAAB   z BABBB

2、解答

将/视为分隔符，利用工具密码机器 (ctftools.com)

解出

1
may be have another decodehhhhaaaaabaabbbaabbaaaaaaaabaababaaaaaaabbabaaabbaaabbaabaaaababaabaaabbabaaabaaabaababbaabbbabaaabababbaaabbabaaabaabaabaaaabbabbaabbaabaabaaabaabaabaababaabbabaaaabbabaabba

看出来后面的是培根密码

再解密

image-20220313153345327

3、注意

仅有a/b构成的密码考虑培根密码

七、混合编码

题目：JiM3NjsmIzEyMjsmIzY5OyYjMTIwOyYjNzk7JiM4MzsmIzU2OyYjMTIwOyYjNzc7JiM2ODsmIzY5OyYjMTE4OyYjNzc7JiM4NDsmIzY1OyYjNTI7JiM3NjsmIzEyMjsmIzEwNzsmIzUzOyYjNzY7JiMxMjI7JiM2OTsmIzEyMDsmIzc3OyYjODM7JiM1NjsmIzEyMDsmIzc3OyYjNjg7JiMxMDc7JiMxMTg7JiM3NzsmIzg0OyYjNjU7JiMxMjA7JiM3NjsmIzEyMjsmIzY5OyYjMTIwOyYjNzg7JiMxMDU7JiM1NjsmIzEyMDsmIzc3OyYjODQ7JiM2OTsmIzExODsmIzc5OyYjODQ7JiM5OTsmIzExODsmIzc3OyYjODQ7JiM2OTsmIzUwOyYjNzY7JiMxMjI7JiM2OTsmIzEyMDsmIzc4OyYjMTA1OyYjNTY7JiM1MzsmIzc4OyYjMTIxOyYjNTY7JiM1MzsmIzc5OyYjODM7JiM1NjsmIzEyMDsmIzc3OyYjNjg7JiM5OTsmIzExODsmIzc5OyYjODQ7JiM5OTsmIzExODsmIzc3OyYjODQ7JiM2OTsmIzExOTsmIzc2OyYjMTIyOyYjNjk7JiMxMTk7JiM3NzsmIzY3OyYjNTY7JiMxMjA7JiM3NzsmIzY4OyYjNjU7JiMxMTg7JiM3NzsmIzg0OyYjNjU7JiMxMjA7JiM3NjsmIzEyMjsmIzY5OyYjMTE5OyYjNzc7JiMxMDU7JiM1NjsmIzEyMDsmIzc3OyYjNjg7JiM2OTsmIzExODsmIzc3OyYjODQ7JiM2OTsmIzExOTsmIzc2OyYjMTIyOyYjMTA3OyYjNTM7JiM3NjsmIzEyMjsmIzY5OyYjMTE5OyYjNzc7JiM4MzsmIzU2OyYjMTIwOyYjNzc7JiM4NDsmIzEwNzsmIzExODsmIzc3OyYjODQ7JiM2OTsmIzEyMDsmIzc2OyYjMTIyOyYjNjk7JiMxMjA7JiM3ODsmIzY3OyYjNTY7JiMxMjA7JiM3NzsmIzY4OyYjMTAzOyYjMTE4OyYjNzc7JiM4NDsmIzY1OyYjMTE5Ow==

1、知识补充

img

2、解答

观察密文，像是用base64加密，解密后出现

1
LzExOS8xMDEvMTA4Lzk5LzExMS8xMDkvMTAxLzExNi8xMTEvOTcvMTE2LzExNi85Ny85OS8xMDcvOTcvMTEwLzEwMC8xMDAvMTAxLzEwMi8xMDEvMTEwLzk5LzEwMS8xMTkvMTExLzExNC8xMDgvMTAw

了解后是Unicode编码，要转到ASCII

Unicode编码转换 | Unicode在线转换 —在线工具 (sojson.com)

1
LzExOS8xMDEvMTA4Lzk5LzExMS8xMDkvMTAxLzExNi8xMTEvOTcvMTE2LzExNi85Ny85OS8xMDcvOTcvMTEwLzEwMC8xMDAvMTAxLzEwMi8xMDEvMTEwLzk5LzEwMS8xMTkvMTExLzExNC8xMDgvMTAw

观察看仍然是一个base64加密

解密后

1
/119/101/108/99/111/109/101/116/111/97/116/116/97/99/107/97/110/100/100/101/102/101/110/99/101/119/111/114/108/100

考虑到flag应全为小写字母，即ASCII码全部大于97，符合条件，对照表格转换

1
welcometoattackanddefenceworld

3、注意

辨识Unicode编码方式

八、easy_RSA

题目：在一次RSA密钥对生成中，假设p=473398607161，q=4511491，e=17
求解出d

1、知识补充

RSA加密原理

步骤 说明 描述 备注
1 找出质数 P 、Q -
2 计算公共模数 N = P * Q -
3 欧拉函数 φ(N) = (P-1)(Q-1) -
4 计算公钥E 1 < E < φ(N) E的取值必须是整数 E 和 φ(N) 必须是互质数
5 计算私钥D E * D % φ(N) = 1 -
6 加密 C ＝ M E mod N C：密文 M：明文
7 解密 M ＝C D mod N C：密文 M：明文

公钥＝(E , N)
私钥＝(D, N)

对外，我们只暴露公钥。

  • 示例

1、找出质数 P 、Q

P = 3 Q = 11

  • 1
  • 2

2、计算公共模数

N = P Q = 3 11 = 33 N = 33

  • 1
  • 2

3、 欧拉函数

φ(N) = (P-1)(Q-1) = 2 * 10 = 20 φ(N) = 20

  • 1
  • 2

4、计算公钥E

1 < E < φ(N) 1 <E < 20

  • 1
  • 2

E 的取值范围 {3, 7, 9, 11, 13, 17, 19}
E的取值必须是整数, E 和 φ(N) 必须是互质数
为了测试，我们取最小的值 E =3
3 和 φ(N) =20 互为质数，满足条件

5、计算私钥D

E D % φ(N) = 1 3 D % 20 = 1

  • 1
  • 2

根据上面可计算出 D = 7

6、公钥加密

我们这里为了演示，就加密一个比较小的数字 M = 2

公式：C ＝ ME mod N

M = 2 E = 3 N = 33

  • 1
  • 2
  • 3

C = 23 % 33 = 8

明文 “2” 经过 RSA 加密后变成了密文 “8”

7、私钥解密

M ＝CD mod N

C = 8 D = 7 N = 33

  • 1
  • 2
  • 3

M = 87 % 33
8 8 8 8 8 8 8=2097152
8 8 8 8 8 8 8 % 33 = 2

密文 “8” 经过 RSA 解密后变成了明文 2。

2、解答

1.先计算欧拉函数
在这里插入图片描述
2.欧拉函数+1再除以17即是私钥
image-20220315135542087

3、注意

理解RSA加密原理

九、easychallenge

题目：附件下载下来发现是一个.pyc 文件

1、知识补充

pyc是一种二进制文件，是由py文件经过编译后，生成的文件，是一种byte code，py文件变成pyc文件后，运行加载的速度会有所提高；另一反面，把py文件编译为pyc文件，从而可以实现部分的源码隐藏，保证了python做商业化软件时的安全性

用uncompyle6这个第三方python反编译器来进行反编译

uncompyle6是一个原生python的跨版本反编译器和fragment反编译器，是decompyle、uncompyle、uncompyle2等的接替者。
image-20220315151418174

2、解答

利用uncompyle6反编译得

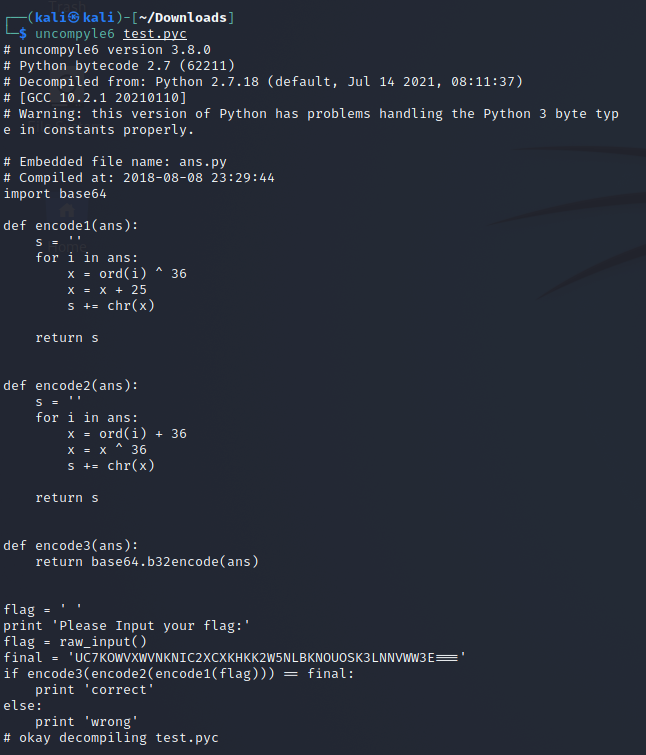
image-20220315142107714

导出代码，修改由于版本不一样的错误：

一共有两个，第一个是print’correct’报错，第二个是flag = raw_input()报错

将 print’correct’改为 print(‘correct’)

将 flag = raw_input() 改为 flag = eval(input())

根据 这个加密运算过程，写出逆过程，将 final 值作为输入 进函数的值，然后以与之前相反的顺序调用函数，最 后输出的值就是 flag

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
##原代码
import base64

def encode1(ans):
    s = ''
    for i in ans:
        x = ord(i) ^ 36
        x = x + 25
        s += chr(x)

    return s


def encode2(ans):
    s = ''
    for i in ans:
        x = ord(i) + 36
        x = x ^ 36
        s += chr(x)

    return s


def encode3(ans):
    return base64.b32encode(ans)


flag = ' '
print (Please Input your flag:)
flag = input()
final = 'UC7KOWVXWVNKNIC2XCXKHKK2W5NLBKNOUOSK3LNNVWW3E==='
if encode3(encode2(encode1(flag))) == final:
    print (correct)
else:
    print (wrong)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
##修改后代码（改顺序）
import base64

def encode1(ans):
    s = ''
    for i in ans:
        x = ord(i) - 25
        x = x ^ 36
        s += chr(x)

    return s


def encode2(ans):
    s = ''
    for i in ans:
        x = ord(i) ^ 36
        x = x - 36
        s += chr(x)

    return s


def encode3(ans):
    return base64.b32decode(ans)

final = 'UC7KOWVXWVNKNIC2XCXKHKK2W5NLBKNOUOSK3LNNVWW3E==='
flag = ' '
flag = encode1(encode2(encode3(final).decode('ISO-8859-1')))
print ("flag={}".format(flag))

3、注意

（1）安装uncompyle6时出现“not on PATH”的问题：

解决：export PATH=/home/kali/.local/bin/:$PATH

（2）发现末尾有’===’，所以应该是 base32

（3）改成 encode3(final).decode(‘ISO-8859-1’)之后，程序顺利运行

？python - “for line in…” results in UnicodeDecodeError: ‘utf-8’ codec can’t decode byte - Stack Overflow

十、转轮机加密

题目：

1: < ZWAXJGDLUBVIQHKYPNTCRMOSFE <
2: < KPBELNACZDTRXMJQOYHGVSFUWI <
3: < BDMAIZVRNSJUWFHTEQGYXPLOCK <
4: < RPLNDVHGFCUKTEBSXQYIZMJWAO <
5: < IHFRLABEUOTSGJVDKCPMNZQWXY <
6: < AMKGHIWPNYCJBFZDRUSLOQXVET <
7: < GWTHSPYBXIZULVKMRAFDCEONJQ <
8: < NOZUTWDCVRJLXKISEFAPMYGHBQ <
9: < XPLTDSRFHENYVUBMCQWAOIKZGJ <
10: < UDNAJFBOWTGVRSCZQKELMXYIHP <
11： < MNBVCXZQWERTPOIUYALSKDJFHG <
12： < LVNCMXZPQOWEIURYTASBKJDFHG <
13： < JZQAWSXCDERFVBGTYHNUMKILOP <

密钥为：2,3,7,5,13,12,9,1,8,10,4,11,6
密文为：NFQKSEVOQOFNP

1、知识补充

加密学技术在几个世纪中不断地发展。托马斯杰斐逊，在17世纪末时，描述发表了一个在加密学中一个重大突破，但理论当时并没有实质建立过。他的发表，称为加密轮，由移动轮上的36个字母环组成，可用于实现复杂的编码上。这个概念是如此的先进，以至于它可以在第二次世界大战末期时，作为美国军事编码的基础。

1.首先我们根据密钥来进行重新排列轮子

2.密钥得数字就代表第几个轮子，如2，3，7，5…代表第一行换成原来第二行得，第二行换成原来第三行得，依次类推

3.排好后根据密文，进行行内排列，如 KPBELNACZDTRXMJQOYHGVSFUWI 进行重新排列后，找到N所在位置，然后重新拼接 ‘NACZDTRXMJQOYHGVSFUWI’+’KPBEL’

4.对所有行排好后按照列取

2、解答

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
#转轮机加密
original_wheel = ['ZWAXJGDLUBVIQHKYPNTCRMOSFE',
                  'PBELNACZDTRXMJQOYHGVSFUWI',
                  'BDMAIZVRNSJUWFHTEQGYXPLOCK',
                  'RPLNDVHGFCUKTEBSXQYIZMJWAO',
                  'IHFRLABEUOTSGJVDKCPMNZQWXY',
                  'AMKGHIWPNYCJBFZDRUSLOQXVET',
                  'GWTHSPYBXIZULVKMRAFDCEONJQ',
                  'NOZUTWDCVRJLXKISEFAPMYGHBQ',
                  'XPLTDSRFHENYVUBMCQWAOIKZGJ',
                  'UDNAJFBOWTGVRSCZQKELMXYIHP',
                  'MNBVCXZQWERTPOIUYALSKDJFHG',
                  'LVNCMXZPQOWEIURYTASBKJDFHG',
                  'JZQAWSXCDERFVBGTYHNUMKILOP ']#所给初始状态的轮转机
shifted_wheel = []
key = [2,3,7,5,13,12,9,1,8,10,4,11,6] #所给密钥
ciphertext = 'NFQKSEVOQOFNP' #所给密文
 
#按照密钥顺序对轮排序
for i in key:
    shifted_wheel.append(original_wheel[i-1])
print('按照密钥重新排序后的轮转机：\n',shifted_wheel)
 
#按照密文顺序转动轮
for i in range(len(shifted_wheel)):
    index = shifted_wheel[i].index(ciphertext[i])
    shifted_wheel[i] = shifted_wheel[i][index:]+shifted_wheel[i][0:index]
print('按照密文重新排序后的轮转机：\n',shifted_wheel)
 
#读取所有恢复的明文
print('输出所有可能的明文：')
for i in range(1,len(shifted_wheel[0])):
    for j in range(len(shifted_wheel)):
        print(shifted_wheel[j][i],end='')
    print('\n')

结合语境，得出答案

3、注意

转轮机原理

十一、Normal_RSA

题目：解压附件得到一个flag.enc文件和一个pubkey.pem文件

1、知识补充

遇到.pem .enc 或者是.der 文件格式时就要用上openssl

在这里插入图片描述

2、解答

首先遇到pubkey.pem，就是rsa 的公钥文件，把该文件拖到虚拟机Linux的桌面上，然后再进入该目录，输入

1
openssl rsa -in pubkey.pem -pubin -modulus -text

-in 是输入文件
-pubin是表示从文件中公钥（因为默认是读取私钥）
附加：-pubout是表示输出公钥（默认是输出私钥）
所以上面也可以换成这个：

1
openssl rsa -in pubkey.pem -pubin -pubout -modulus -text

结果都是一样的。
-text 是输出密钥的各种组件信息以及密钥文件本身的文本（但是不会直接输出公钥，所以需要下一句）
-modulus 是输出密钥模数（就是输出N）模N
实际上-text命令提供e,-modulus命令提供N

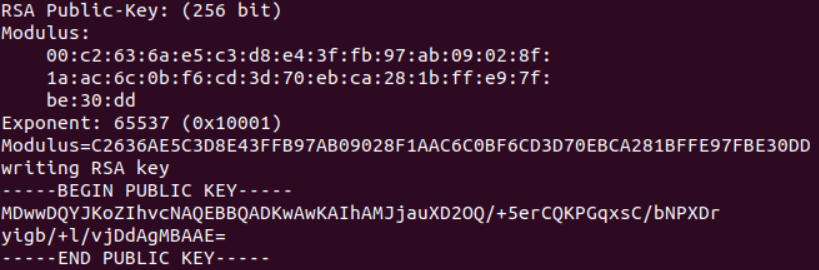
image-20220317173931445

图中的Exponent就是e，Modulus就是N。
-noout 命令是不输出密钥文件的文本内容，即上图中—BEGIN PUBLIC KEY–到—END PUBLIC KEY —的内容。
所以想要输出的内容美观一点，只需输入

1
openssl rsa -in pubkey.pem -pubin -modulus -noout

rsatool是一个简单的计算工具。

有两种输入方法：一是输入p和q，另一种是输入n和d。之后让它生成一个完整的密钥文件（p,q,n,e,d）
使用方法：
一.输入p和q

1
python rsatool.py -f DER -o key.pem -p 4184799299 -q 3303891593

二.输入n和d

1
python  rsatool.py -f PEM -o key.pem -n 13826123222358393307 -d9793706120266356337

-f是输出文件的格式
-o是输出文件的名称

最后我们可以得到key.pem 这个密钥文件，注意这是.pem文件，所以又得用openssl来操作。
解密：（假设待解密文件是flag.enc）

1
openssl rsautl -decrypt -in flag.enc  -inkey key.pem

-inkey 是用的密钥文件
-decrypt是解密
最后解密结果就会输出来了

3、注意

遇到.pem .enc 或者是.der 文件格式时就要用上openssl了，一般都是给公钥文件以及flag文件让你求flag。

十二、easy_ECC

题目：已知椭圆曲线加密Ep(a,b)参数为

p = 15424654874903

a = 16546484

b = 4548674875

G(6478678675,5636379357093)

私钥为

k = 546768

求公钥K(x,y)

1、知识补充

椭圆曲线加密算法，即：Elliptic Curve Cryptography，简称ECC，是基于椭圆曲线数学理论实现的一种非对称加密算法。相比RSA，ECC优势是可以使用更短的密钥，来实现与RSA相当或更高的安全。据研究，160位ECC加密安全性相当于1024位RSA加密，210位ECC加密安全性相当于2048位RSA加密。

椭圆曲线

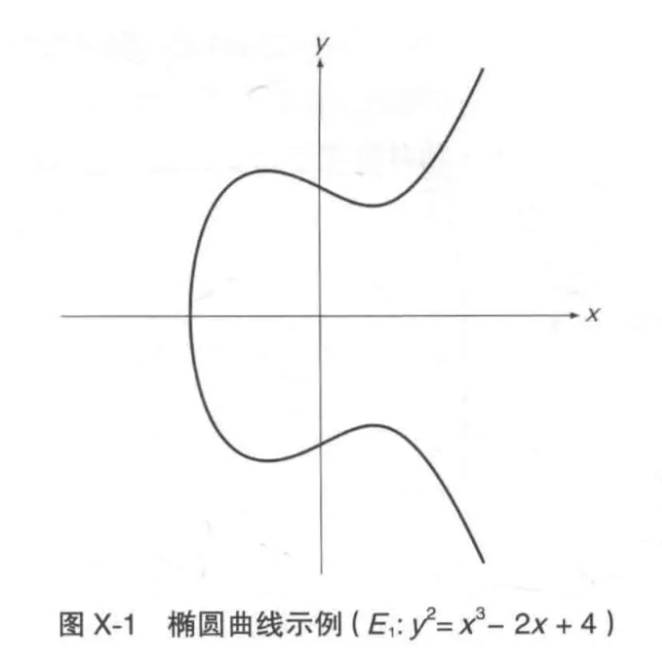
一般情况下，椭圆曲线可用下列方程式来表示，其中a,b,c,d为系数。

E:y2=ax3+ bx2+cx+d

例如，当a=1,b=0,c=-2,d=4时，所得到的椭圆曲线为:

E:y2=x3-2x+4

该椭圆曲线E的图像如图X-1所示，可以看出根本就不是椭圆形。

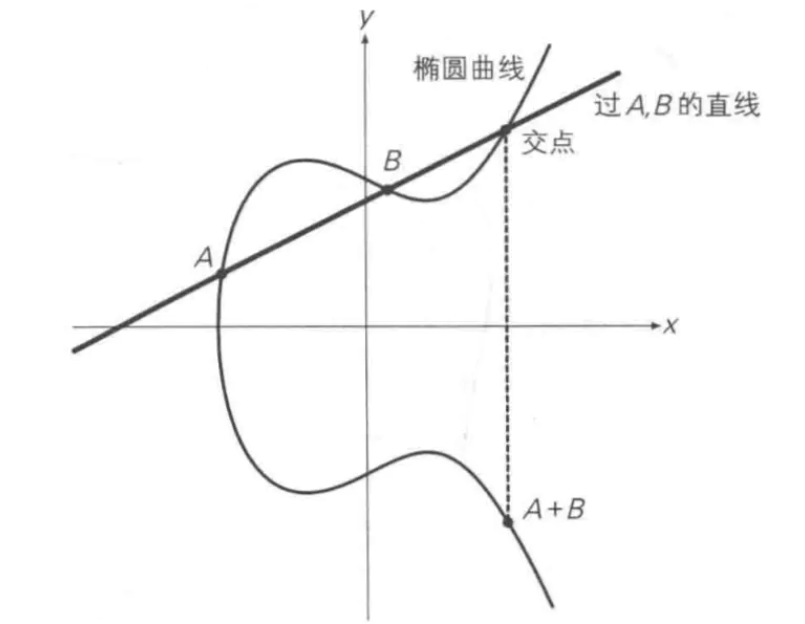
定义椭圆曲线的运算规则

加法

过曲线上的两点A、B画一条直线，找到直线与椭圆曲线的交点，交点关于x轴对称位置的点，定义为A+B，即为加法。如下图所示：A + B = C

二倍运算

上述方法无法解释A + A，即两点重合的情况。因此在这种情况下，将椭圆曲线在A点的切线，与椭圆曲线的交点，交点关于x轴对称位置的点，定义为A + A，即2A，即为二倍运算。

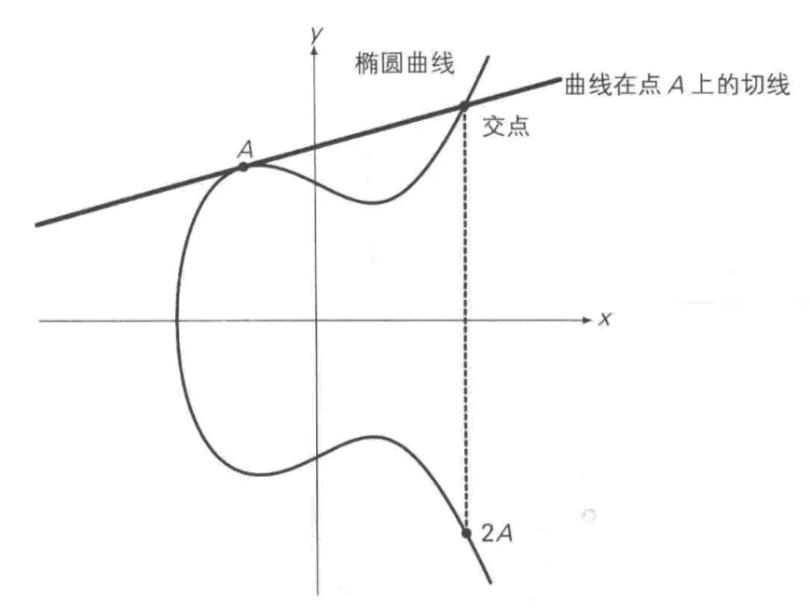
正负取反

将A关于x轴对称位置的点定义为-A，即椭圆曲线的正负取反运算。如下图所示：

无穷远点

如果将A与-A相加，过A与-A的直线平行于y轴，可以认为直线与椭圆曲线相交于无穷远点。

综上，定义了A+B、2A运算，因此给定椭圆曲线的某一点G，可以求出2G、3G（即G + 2G）、4G……。即：当给定G点时，已知x，求xG点并不困难。反之，已知xG点，求x则非常困难。此即为椭圆曲线加密算法背后的数学原理。

有限域上的椭圆曲线运算

椭圆曲线要形成一条光滑的曲线，要求x,y取值均为实数，即实数域上的椭圆曲线。但椭圆曲线加密算法，并非使用实数域，而是使用有限域。按数论定义，有限域GF(p)指给定某个质数p，由0、1、2……p-1共p个元素组成的整数集合中定义的加减乘除运算。

假设椭圆曲线为y² = x³ + x + 1，其在有限域GF(23)上时，写作：　　y² ≡ x³ + x + 1 (mod 23)

此时，椭圆曲线不再是一条光滑曲线，而是一些不连续的点，如下图所示。以点(1,7)为例，7² ≡ 1³ + 1 + 1 ≡ 3 (mod 23)。如此还有如下点：

(0,1) (0,22)　　(1,7) (1,16)　　(3,10) (3,13)　　(4,0)　　(5,4) (5,19)　　(6,4) (6,19)　　(7,11) (7,12)　　(9,7) (9,16)　　(11,3) (11,20)　　等等。

另外，如果P(x,y)为椭圆曲线上的点，则-P即(x,-y)也为椭圆曲线上的点。如点P(0,1)，-P=(0,-1)=(0,22)也为椭圆曲线上的点。

计算xG

相关公式如下：　　有限域GF(p)上的椭圆曲线y² = x³ + ax + b，若P(Xp, Yp), Q(Xq, Yq)，且P≠-Q，则R(Xr,Yr) = P+Q 由如下规则确定：

Xr = (λ² - Xp - Xq) mod p　　Yr = (λ(Xp - Xr) - Yp) mod p　　其中λ = (Yq - Yp)/(Xq - Xp) mod p（若P≠Q）, λ = (3Xp² + a)/2Yp mod p（若P=Q）

因此，有限域GF(23)上的椭圆曲线y² ≡ x³ + x + 1 (mod 23)，假设以(0,1)为G点，计算2G、3G、4G…xG等等，方法如下：

计算2G：　　λ = (3x0² + 1)/2x1 mod 23 = (1/2) mod 23 = 12　　Xr = (12² - 0 - 0) mod 23 = 6　　Yr = (12(0 - 6) - 1) mod 23 = 19　　即2G为点(6,19)

计算3G：　　3G = G + 2G，即(0,1) + (6,19)　　λ = (19 - 1)/(6 - 0) mod 23 = 3　　Xr = (3² - 0 - 6) mod 23 = 3　　Yr = (3(0 - 3) - 1) mod 23 = 13　　即3G为点(3, 13)

同理计算4G、5G…xG　

椭圆曲线加解密算法原理

建立基于椭圆曲线的加密机制，需要找到类似RSA质因子分解或其他求离散对数这样的难题。而椭圆曲线上的已知G和xG求x，是非常困难的，此即为椭圆曲线上的的离散对数问题。此处x即为私钥，xG即为公钥。

椭圆曲线加密算法原理如下：

设私钥、公钥分别为k、K，即K = kG，其中G为G点。

公钥加密：　　选择随机数r，将消息M生成密文C，该密文是一个点对，即：　　C = {rG, M+rK}，其中K为公钥

私钥解密：　　M + rK - k(rG) = M + r(kG) - k(rG) = M　　其中k、K分别为私钥、公钥。

椭圆曲线签名算法原理

椭圆曲线签名算法，即ECDSA。　　设私钥、公钥分别为k、K，即K = kG，其中G为G点。

私钥签名：　　1、选择随机数r，计算点rG(x, y)。　　2、根据随机数r、消息M的哈希h、私钥k，计算s = (h + kx)/r。　　3、将消息M、和签名{rG, s}发给接收方。

公钥验证签名：　　1、接收方收到消息M、以及签名{rG=(x,y), s}。　　2、根据消息求哈希h。　　3、使用发送方公钥K计算：hG/s + xK/s，并与rG比较，如相等即验签成功。

原理如下：　　hG/s + xK/s = hG/s + x(kG)/s = (h+xk)G/s　　= r(h+xk)G / (h+kx) = rG

签名过程

假设要签名的消息是一个字符串：“Hello World!”。DSA签名的第一个步骤是对待签名的消息生成一个消息摘要。不同的签名算法使用不同的消息摘要算法。而ECDSA256使用SHA256生成256比特的摘要。
摘要生成结束后，应用签名算法对摘要进行签名：
产生一个随机数k
利用随机数k，计算出两个大数r和s。将r和s拼在一起就构成了对消息摘要的签名。
这里需要注意的是，因为随机数k的存在，对于同一条消息，使用同一个算法，产生的签名是不一样的。从函数的角度来理解，签名函数对同样的输入会产生不同的输出。因为函数内部会将随机值混入签名的过程。

验证过程

关于验证过程，这里不讨论它的算法细节。从宏观上看，消息的接收方从签名中分离出r和s，然后利用公开的密钥信息和s计算出r。如果计算出的r和接收到的r值相同，则表示验证成功。否则，表示验证失败。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
package main

import (
    "fmt"
    "crypto/ecdsa"
    "crypto/elliptic"
    "crypto/rand"
    "crypto/sha256"
    "math/big"
)

func main() {
    //明文 
    message := []byte("Hello world")
    
    key, err := NewSigningKey()
    if err != nil {
        return
    }

    signature, err := Sign(message, key)

    fmt.Printf("签名后：%x\n", signature)
    if err != nil {
        return
    }

    if !Verify(message, signature, &key.PublicKey) {
        fmt.Println("验证失败！")
        return
    }else{
        fmt.Println("验证成功！")
    }
}

func NewSigningKey() (*ecdsa.PrivateKey, error) {
    key, err := ecdsa.GenerateKey(elliptic.P256(), rand.Reader)
    return key, err
}

// Sign signs arbitrary data using ECDSA.
func Sign(data []byte, privkey *ecdsa.PrivateKey) ([]byte, error) {
    // hash message
    digest := sha256.Sum256(data)

    // sign the hash
    r, s, err := ecdsa.Sign(rand.Reader, privkey, digest[:])
    if err != nil {
        return nil, err
    }

    // encode the signature {R, S}
    // big.Int.Bytes() will need padding in the case of leading zero bytes
    params := privkey.Curve.Params()
    curveOrderByteSize := params.P.BitLen() / 8
    rBytes, sBytes := r.Bytes(), s.Bytes()
    signature := make([]byte, curveOrderByteSize*2)
    copy(signature[curveOrderByteSize-len(rBytes):], rBytes)
    copy(signature[curveOrderByteSize*2-len(sBytes):], sBytes)

    return signature, nil
}

// Verify checks a raw ECDSA signature.
// Returns true if it's valid and false if not.
func Verify(data, signature []byte, pubkey *ecdsa.PublicKey) bool {
    // hash message
    digest := sha256.Sum256(data)

    curveOrderByteSize := pubkey.Curve.Params().P.BitLen() / 8

    r, s := new(big.Int), new(big.Int)
    r.SetBytes(signature[:curveOrderByteSize])
    s.SetBytes(signature[curveOrderByteSize:])

    return ecdsa.Verify(pubkey, digest[:], r, s)
}

参考：椭圆曲线加密算法 - 简书 (jianshu.com)

2、解答

使用脚本

脚本一（欧几里得）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
#椭圆曲线
import collections
import random
 
EllipticCurve = collections.namedtuple('EllipticCurve', 'name p a b g n h')
 
curve = EllipticCurve(
   'secp256k1',
   # Field characteristic.
   p=int(input('p=')),
   # Curve coefficients.
   a=int(input('a=')),
   b=int(input('b=')),
   # Base point.
   g=(int(input('Gx=')),
      int(input('Gy='))),
   # Subgroup order.
   n=int(input('k=')),
   # Subgroup cofactor.
   h=1,
)
 
 
# Modular arithmetic ##########################################################
 
def inverse_mod(k, p):
   """Returns the inverse of k modulo p.
  This function returns the only integer x such that (x * k) % p == 1.
  k must be non-zero and p must be a prime.
  """
   if k == 0:
       raise ZeroDivisionError('division by zero')
 
   if k < 0:
       # k ** -1 = p - (-k) ** -1 (mod p)
       return p - inverse_mod(-k, p)
 
   # Extended Euclidean algorithm.
   s, old_s = 0, 1
   t, old_t = 1, 0
   r, old_r = p, k
 
   while r != 0:
       quotient = old_r // r
       old_r, r = r, old_r - quotient * r
       old_s, s = s, old_s - quotient * s
       old_t, t = t, old_t - quotient * t
 
   gcd, x, y = old_r, old_s, old_t
 
   assert gcd == 1
   assert (k * x) % p == 1
 
   return x % p
 
 
# Functions that work on curve points #########################################
 
def is_on_curve(point):
   """Returns True if the given point lies on the elliptic curve."""
   if point is None:
       # None represents the point at infinity.
       return True
 
   x, y = point
 
   return (y * y - x * x * x - curve.a * x - curve.b) % curve.p == 0
 
 
def point_neg(point):
   """Returns -point."""
   assert is_on_curve(point)
 
   if point is None:
       # -0 = 0
       return None
 
   x, y = point
   result = (x, -y % curve.p)
 
   assert is_on_curve(result)
 
   return result
 
 
def point_add(point1, point2):
   """Returns the result of point1 + point2 according to the group law."""
   assert is_on_curve(point1)
   assert is_on_curve(point2)
 
   if point1 is None:
       # 0 + point2 = point2
       return point2
   if point2 is None:
       # point1 + 0 = point1
       return point1
 
   x1, y1 = point1
   x2, y2 = point2
 
   if x1 == x2 and y1 != y2:
       # point1 + (-point1) = 0
       return None
 
   if x1 == x2:
       # This is the case point1 == point2.
       m = (3 * x1 * x1 + curve.a) * inverse_mod(2 * y1, curve.p)
   else:
       # This is the case point1 != point2.
       m = (y1 - y2) * inverse_mod(x1 - x2, curve.p)
 
   x3 = m * m - x1 - x2
   y3 = y1 + m * (x3 - x1)
   result = (x3 % curve.p,
             -y3 % curve.p)
 
   assert is_on_curve(result)
 
   return result
 
 
def scalar_mult(k, point):
   """Returns k * point computed using the double and point_add algorithm."""
   assert is_on_curve(point)
 
 
 
   if k < 0:
       # k * point = -k * (-point)
       return scalar_mult(-k, point_neg(point))
 
   result = None
   addend = point
 
   while k:
       if k & 1:
           # Add.
           result = point_add(result, addend)
 
       # Double.
       addend = point_add(addend, addend)
 
       k >>= 1
 
   assert is_on_curve(result)
 
   return result
 
 
# Keypair generation and ECDHE ################################################
 
def make_keypair():
   """Generates a random private-public key pair."""
   private_key = curve.n
   public_key = scalar_mult(private_key, curve.g)
 
   return private_key, public_key
 
 
 
private_key, public_key = make_keypair()
print("private key:", hex(private_key))
print("public key: (0x{:x}, 0x{:x})".format(*public_key))


脚本二（费马小定理）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
#求 x 的 y 次方的模 
def power(x, y, mod): 
    r = 1 
    while( y ): 
        if y & 1: 
            r = (r * x) % mod 
        x = (x * x) % mod 
        y >>= 1 
    return r 
Gx = 6478678675 
Gy = 5636379357093 
a = 16546484 
b = 4548674875 
p = 15424654874903 
k = 546768 
x = Gx 
y = Gy 
for i in range(k-1): 
    if (x==Gx and y==Gy): 
        inv = power(2*Gy, p-2,p) 
        temp = (3*Gx*Gx+a)*inv%p 
    else: 
        inv = power((x-Gx), p-2,p) 
        temp = (y-Gy)*inv%p 
    #print(temp) 
    xr = (temp*temp-Gx-x)%p 
    yr = (temp*(x-xr)-y)%p 
    #print(i,xr,yr) 
    x = xr 
    y = yr 
print(x+y)

3、注意

对原理的理解？

几个网站：

CTF常见编码及加解密（超全） - ruoli-s - 博客园 (cnblogs.com)

识别密文加密方式K’illCode的博客-CSDN博客识别加密方式